The Queue

What is a Queue ?

A Queue is a "First in, First out" (FIFO) data structure where the first inserted elemen is the first removed. It has two core operations :

• Enqueue: Insert an element at the back of the queue.
• Dequeue: Remove the element at the front of the queue.

The queue has a "Front" and a "Back". We enqueue elements at the back of the queue and dequeue elements at the front of the queue :

A Queue can have different purpose and therefore different implementations, for example :

• Priority Queue where the insertion index of the element is based on its priority or up to the dequeuing process (for unsorted queues). In such case the queue would always dequeue the item with the highest or lowest (depending of the sorting implementation) priority.

• Circular Queue, where the front of the queue points back to the back of the queue, making it circular (such queues must have a specific length).

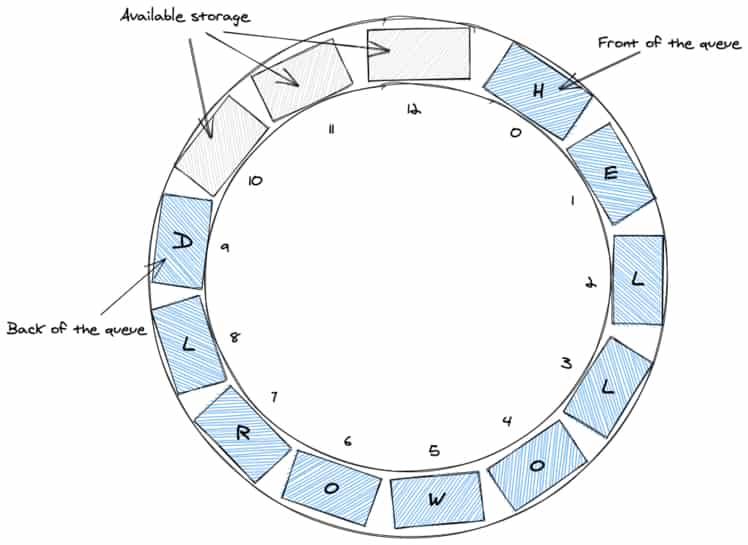
In this post we will implement both a simple queue and then a priorty queue.

Benefits

For a simple queue, the enqueue and dequeue operations are very efficient (constant time operations O(1)) as there is no needed interactions with the rest of the queue.

Downsides

In the same way as a stack, searching a simple queue is an inefficient operation as it requires to dequeue elements of the queue until the search target is found making it O(n).

Practical uses in web development

A good example of a queue usage is rate limiting to ensure the consistent service of user request under heavy load but keep servicing user request in a FIFO manner.

Basic Queue

Basic methods

We will implement our simple Queue using Typescript class syntax and an empty array to store out data. The beginning of our array we be our queue back, and the end of our array will be our queue front.

export class Queue<T> {
  queue: Array<T>
  constructor() {
    this.queue = []
  }
}

• Enqueue()

The enqueue insert an element at the back of our queue and therefore at the beginning of our array, we will implement this operations with the unshift() array method.

enqueue(value: T) {
    this.queue.unshift(value);
 }

• Dequeue()

The dequeue get the queue last index, test its validity, and leverage the pop() array method to return and remove the item at the front of the queue.

dequeue() {
    if (this.queue.length <= 0) return null;
    return this.queue.pop();
}

• Peek()

The peek get the last item and return correspond item in the queue or null if none is found

peek() {
    const lastIndex = this.queue.length - 1;
    if (lastIndex < 0) return null;
    return this.queue[lastIndex];
  }

Helpers methods

Helpers methods such as clear, isEmpty, and print can also be added.

isEmpty() {
    return this.queue.length === 0;
}
 
clear() {
    this.queue = [];
}
 
print() {
    if (this.queue === []) {
      console.log('Empty Queue');
    } else {
      this.queue.forEach((item, index) =>
        console.log(`${index} : ${JSON.stringify(item, undefined, 2)}`)
      );
    }
}
 

More advanced methods

• Reverse()

The reverse method we will implement uses a recursion. Our function will get the item at the front of the queue, dequeue it, recursively call itself to keep traversing the queue and then adding back our item at the back of queue.

reverse(queue: Queue<T>): Queue<T> {
    if (queue.isEmpty()) return queue;
    const front = queue.peek();
    queue.dequeue();
    queue = this.reverse(queue);
    queue.enqueue(front as T);
    return queue;
  }

Priority Queue

One of the challenges of implementing a Priority Queue is handling the queue sorting because an unsorted priority queue would required additional operations to ensure the dequeuing of the highest priority element of the queue and therefore be slower. In this implementation we will enforce the queue sorting during the enqueuing of elements.

Basic methods

Our Priority Queue implementation will use Typescript class Syntax and an empty array to store out data. The queue elements will be sorted by priority : lowest at the back of the queue and highest at the front of the queue.

interface BaseElement {
  priority: number
}
 
export class PriorityQueue<Element extends BaseElement> {
  queue: Array<Element>
  constructor() {
    this.queue = []
  }
}

• Enqueue()

Because our enqueue method enforces the queue sorting, it will be the most complex method we will implement in our priority queue.

Our enqueue function will push a new element at the back of the queue if the queue is empty or if the new element priority is higher than the element at the front of the queue. If the new element priority is lower than the queue front element's, we need to find the correct insertion index of the new element in the queue using the lowerbound function. We then insert the new element in the queue using the slice() array method.

  enqueue(element: Element) {
    // Empty Queue or Queue last elem prio <= elem prio => insert item at the end of the array
    if (
      this.queue.length === 0 ||
      this.queue[this.queue.length - 1].priority <= element.priority
    ) {
      this.queue.push(element);
      return;
    }
 
    // Need to find the correct insertion index given the element priority
    const insertionIndex = lowerBound(
      this.queue,
      element,
      (a: Element, b: Element) => a.priority - b.priority
    );
    this.queue.splice(insertionIndex, 0, element);
  }

• Dequeue()

The dequeue operation is really simple as we only pop() and return the last element of the array (the one with the highest priority).

  dequeue() {
    return this.queue.pop();
  }

• Reverse()

Our reverse methods is quite similar to the simple queue one, except that we don't re-enqueue the element at the front of the queue because our enqueue methods sorting logic. Instead we insert it at the back of the queue with unshift() array method.

reverse(queue: PriorityQueue<Element>): PriorityQueue<Element> {
    if (queue.isEmpty()) return queue;
    const front = queue.peek();
    queue.dequeue();
    queue = this.reverse(queue);
    this.queue.unshift(front as Element);
    return queue;
  }